跳到主要内容

面试题39. 数组中出现次数超过一半的数字

题目描述​

做题链接：面试题39. 数组中出现次数超过一半的数字

解题思路​

参考：https://leetcode-cn.com/problems/shu-zu-zhong-chu-xian-ci-shu-chao-guo-yi-ban-de-shu-zi-lcof/solution/mian-shi-ti-39-shu-zu-zhong-chu-xian-ci-shu-chao-3/

方法一： 哈希表统计法​

遍历数组 nums ，用 HashMap 统计各数字的数量，最终超过数组长度一半的数字则为众数。此方法时间和空间复杂度均为 $O(N)$

方法二：数组排序法​

将数组 nums 排序，由于众数的数量超过数组长度一半，因此 数组中点的元素 一定为众数。此方法时间复杂度 $O(N log_2 N)$

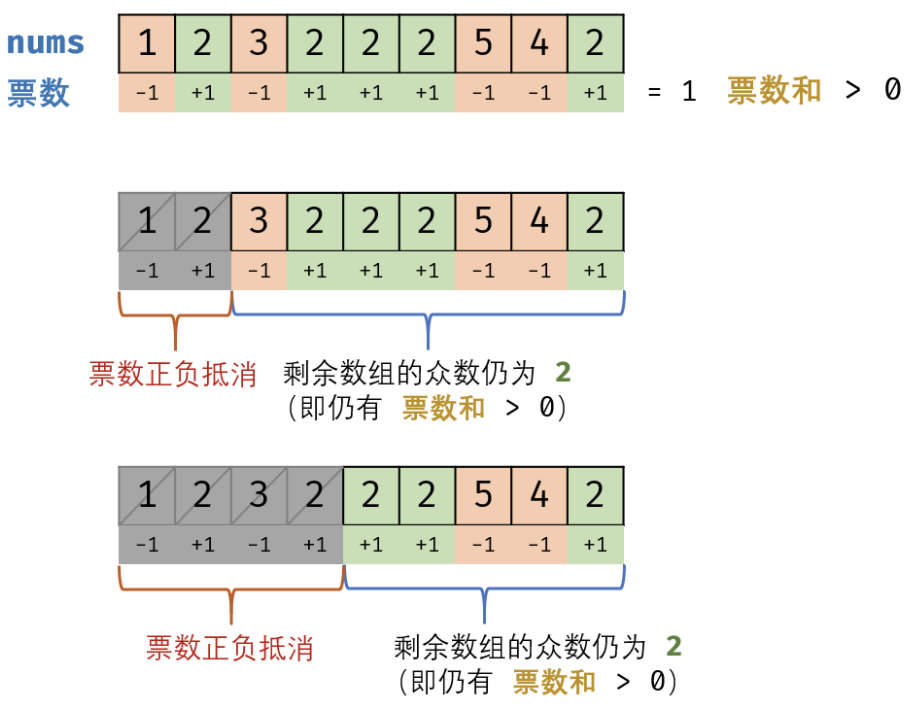
方法三：摩尔投票法​

核心理念为 “正负抵消” ；

时间和空间复杂度分别为 $O(N)$ 和 $O(1)$；是本题的最佳解法。

代码​

方法一：哈希表统计法

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        d = {}
        for num in nums:
            d[num] = d[num] + 1 if num in d else 1
            
        for k, v in d.items():
            if v > len(nums) >> 1:
                return k

方法二：数组排序法

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        nums.sort()
        return nums[len(nums) >> 1]

方法三：摩尔投票法

由于题目中已经保证了一定存在众数，所以后面的验证代码也可以省略

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        votes, count = 0, 0
        for num in nums:
            if votes == 0: x = num
            votes += 1 if num == x else -1
        # 验证 x 是否为众数
        for num in nums:
            if num == x: count += 1
        return x if count > len(nums) // 2 else 0 # 当无众数时返回 0