面试题62. 圆圈中最后剩下的数字【困难】
题目描述
0,1,,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
解题思路&代码
方法一:模拟法
完全模拟题目操作,但是由于 Python 中删除节点的时间复杂度 $O(N)$ ,共要删除 $N-1$ 次,故时间复杂度为 $O(N^2)$,这会导致超时。
根据 Java解决约瑟夫环问题,告诉你为什么模拟会超时! 这一篇文章,可以发现,使用模拟法会导致超时。但是采用 Java 中的 ArrayList 类型能 AC。
不过从时间复杂度上分析:
| 查找复杂度 | 删除复杂度 | 总复杂度 | |
|---|---|---|---|
| ArrayList | O(1) | O(n) | O(n) |
| LinkedList | O(n) | O(1) | O(n) |
无论采用 ArrayList 或是 LinkedList 的时间复杂度都是一样的。只是作者在研究源码发现,Java 的 remove 是对连续内存空间的拷贝,可以通过AC。
不过这类方法我们还是不准备采用,下面给出 连续存储 和 链式存储 的代码
代码
代码一:Python 连续存储【List 类型】
# 2080 ms 勉强 AC
class Solution:
def lastRemaining(self, n: int, m: int) -> int:
s = list(range(n))
i, j = 0, n
for _ in range(n - 1):
i = (i + m - 1) % j
s.pop(i) # 删除节点操作为 O(N)
j -= 1
return s[0]
代码二:双端队列【deque】
# 超时
class Solution:
def lastRemaining(self, n: int, m: int) -> int:
if n < 1:
return -1
queue = collections.deque()
for i in range(n):
queue.append(i)
while len(queue) > 1:
for _ in range(m - 1): # 走第 m - 1步
queue.append(queue.popleft())
queue.popleft() # 击鼓传花,传到 第 m 个人的头上
return queue[0]
代码三:Python 链式存储
# 超时
class Node:
def __init__(self, value):
self.value = value
self.next = None
def create_nodes(n):
head = Node(0)
pre = head
for i in range(1, n):
new_node = Node(i)
pre.next = new_node
pre = pre.next
pre.next = head # 连接头,形成闭环
return head
class Solution:
def lastRemaining(self, n: int, m: int) -> int:
if n == 1: return 0
head = create_nodes(n)
pre = None
cur = head
while cur != cur.next: # 若 cur == cur.next 那么代表只有一个节点
for i in range(m - 1): # 删除第 m 个,先走 m - 1 步
pre = cur
cur = cur.next
print(cur.value) # 输出删除的节点
pre.next = cur.next # 删除 cur 这一节点
cur = pre.next
return cur.value
方法二:分析数字规律
详细解答,请移步 换个角度举例解决约瑟夫环
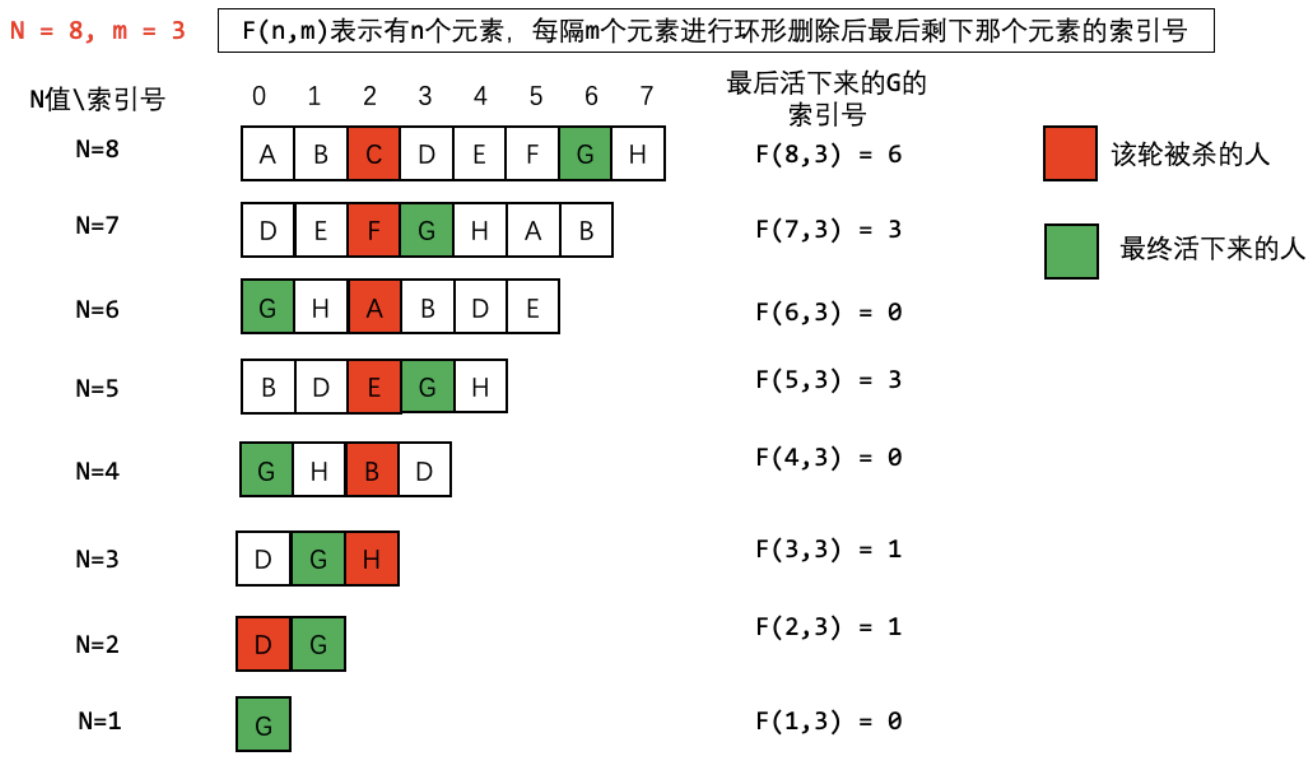
可以知道,最后的答案一定是位于 数据的0位置,所以可以总结出 逆推公式: $$ f(n,m) = \begin{cases} 0 & n = 1\ (f(n-1, m)+m)%n & n>1\ \end{cases} $$
代码
class Solution:
def lastRemaining(self, n: int, m: int) -> int:
pos = 0
for i in range(2, n + 1):
pos = (pos + m) % i
return pos