面试题29. 顺时针打印矩阵

题目描述

做题链接：面试题29. 顺时针打印矩阵

解题思路

方法一： 模拟法——利用访问矩阵

不动脑子的方法，利用 visited 记录走过的点。

• 如果走到的点出现

  • 越界
  • 走过

  就切换方向

• 根据矩阵的大小，可知，只需要走 n * m 次

方法二：寻找规律

规律1

可以通过观察，发现每次 横向移动的时候，移动的长度会减一。纵向移动同样如此。

如一个 $3 \times 3$ 的矩阵，规律为：向右移动3次，向下移动2次，向左移动2次，向上移动1次，向右移动1次。

我们给横向移动设置初始值值 3，纵向移动 2。每次移动完了就减一。

这里需要考虑终止条件的位置：一定是在移动之前检查本方向是否已终止

规律2

上面的代码是从2个方向上去考虑，也可以直接从4个方向上去考虑。这里参考的是 大神思路

通过设置 l, r, t, b 记录上下左右四个方程的初始位置。这里退出的条件是，t > b， l > r

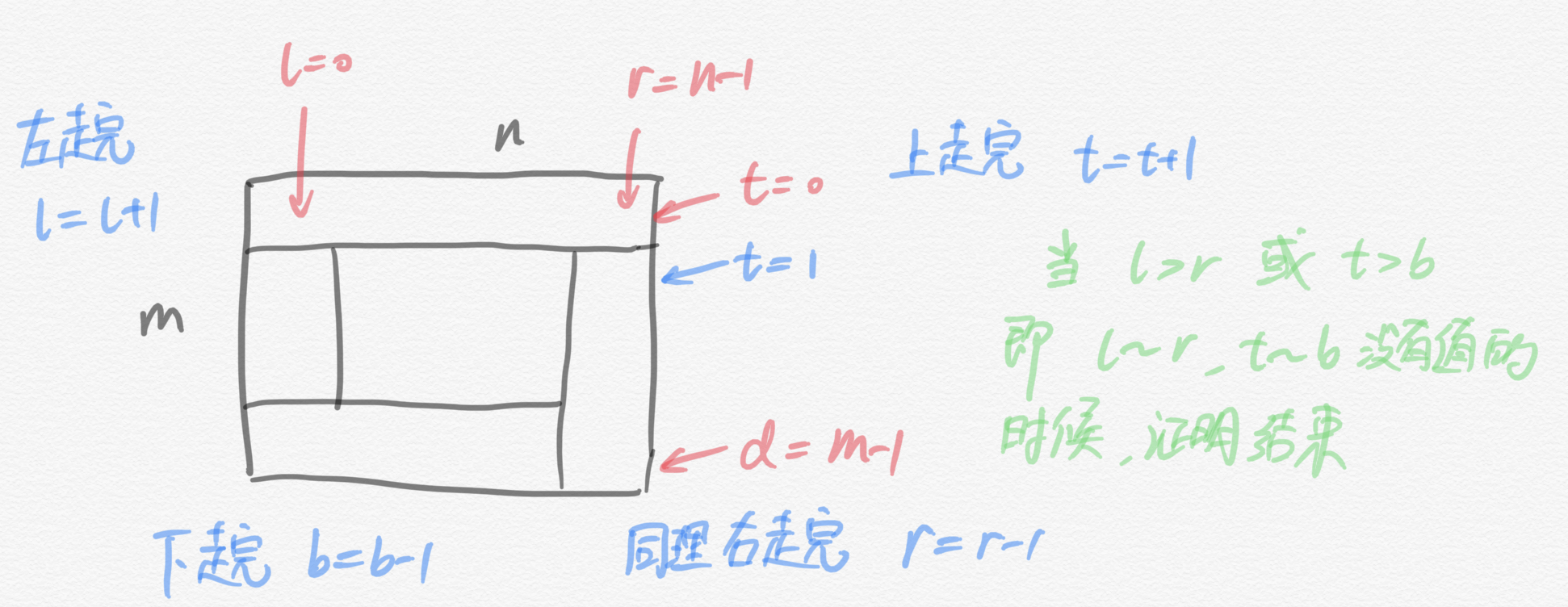
代码

代码1：模拟法

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix: return []
        n, m = len(matrix[0]), len(matrix)
        direction = [(1, 0), (0, 1), (-1, 0), (0, -1)] # 右下左上
        dflag = 0  # 初始方向向右
        res = []
        x, y = -1, 0 # 初始位置
        visited = set()
        for i in range(n * m):
            if x + direction[dflag][0] < 0 or \
               x + direction[dflag][0] >= n or \
               y + direction[dflag][1] < 0 or \
               y + direction[dflag][1] >= m or \
               (x + direction[dflag][0], y + direction[dflag][1]) in visited:
               dflag = (dflag + 1) % 4

            x = x + direction[dflag][0]
            y = y + direction[dflag][1]
            visited.add((x, y))
            res.append(matrix[y][x])
        return res 

代码2： 寻找规律--2方向

class Solution:
      def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
          if not matrix: return []
          xlen, ylen = len(matrix[0]), len(matrix) - 1
          x, y = -1, 0  
          direction = [(1, 0), (0, 1), (-1, 0), (0, -1)] # 右下左上
          dflag = 0
          ret = []
          while True:
              if not xlen: break # 在横向移动之前，检查能否移动，不能的话一定是代表结束
              for _ in range(xlen): # 横向打印
                  x = x + direction[dflag][0]
                  y = y + direction[dflag][1]
                  ret.append(matrix[y][x])
              
              xlen -= 1
              dflag = (dflag + 1) % 4
              
              if not ylen: break # 在纵向向移动之前，检查能否移动，不能的话一定是代表结束
              for _ in range(ylen): # 横向打印
                  x = x + direction[dflag][0]
                  y = y + direction[dflag][1]
                  ret.append(matrix[y][x])
              ylen -= 1
              dflag = (dflag + 1) % 4
          return ret

代码2：寻找规律--4方向

class Solution:
    def spiralOrder(self, matrix:[[int]]) -> [int]:
        if not matrix: return []
        l, r, t, b, res = 0, len(matrix[0]) - 1, 0, len(matrix) - 1, []
        while True:
            for i in range(l, r + 1): res.append(matrix[t][i]) # left to right
            t += 1
            if t > b: break
            for i in range(t, b + 1): res.append(matrix[i][r]) # top to bottom
            r -= 1
            if l > r: break
            for i in range(r, l - 1, -1): res.append(matrix[b][i]) # right to left
            b -= 1
            if t > b: break
            for i in range(b, t - 1, -1): res.append(matrix[i][l]) # bottom to top
            l += 1
            if l > r: break
        return res

# 作者：jyd
# 链接：https://leetcode-cn.com/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/solution/mian-shi-ti-29-shun-shi-zhen-da-yin-ju-zhen-she-di/