面试题13. 机器人的运动范围

题目描述

做题链接：面试题13. 机器人的运动范围

机器人每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。问最大能到达多少格子

解题思路

方法一：DFS + 剪枝改进

上一题同样是 DFS 算法，其中提到一定要注意 状态回溯 。本题则不同，因为是求的 最多访问到的格子， 最多访问的路径 。所以 辅助矩阵 visited 是记录访问到的格子，最后返回的结果也是 len(visited)

• 终止条件： 下标越界、题目条件限制、节点已访问
• 计算节点位数和的方法可以尝试 memory 记忆矩阵做缓存
• 剪枝体现在：根据题意，只需要访问 右、下 两个方向即可。

方法二：DFS + 数位和计算方式改进

参考：Krahets-解题

Krahets's Blog 这个大神些的东西，真的比原书的作者写的解法好，而且是python版

数位和增量公式：

s_x + 1 if (x + 1) % 10 else s_x - 8

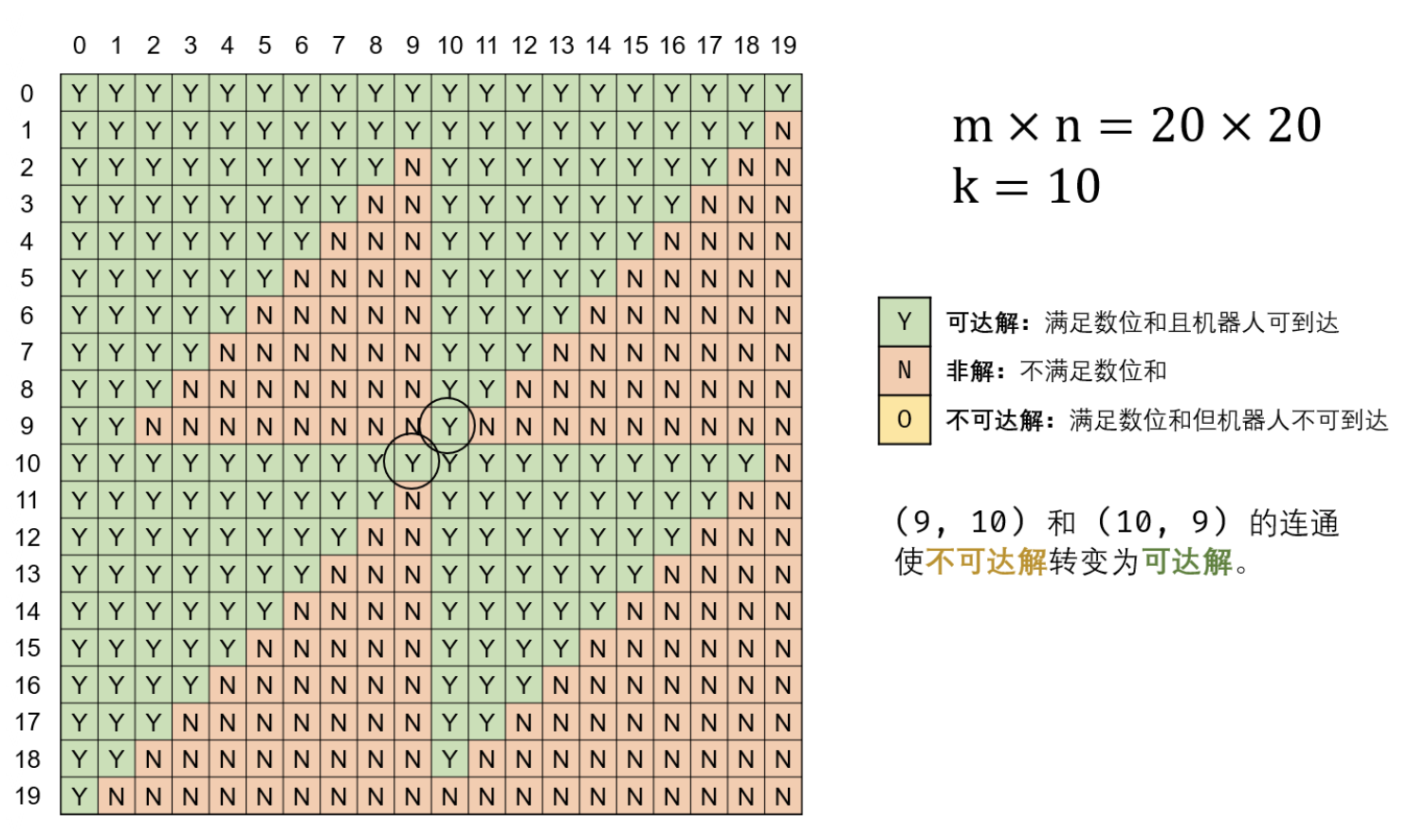
方法三：BFS + 数位和改进

可以看出，本题只是判断某一个格子能不能走到，没有回溯的步骤，即没有 visited.remove(x, y)

故也可以用 BFS 方法实现。

两种计算数位和的方式

# 循环取余
def cal_digit(x):
    if not x in memory:
        ret, y = 0, x
        while y:
            ret += y % 10
            y = y // 10
        memory[x] = ret
    return memory[x]

# 字符串计算
def cal_digit(x):
    if not x in memory:
       ret = sum([int(_) for _ in str(x)])
       memory[x] = ret
    return memory[x]

代码

方法一：DFS改进

class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        def cal_digit(x):
            if not x in memory:
                ret = sum([int(_) for _ in str(x)])
                memory[x] = ret
            return memory[x]

        def dfs(i, j):
            if i >= m or j >=n: return  # 下表越界
            if cal_digit(i) + cal_digit(j)> k: return # 题目条件限制 
            if (i, j) in visited: return # 节点已访问过
            visited.append((i, j))
            dfs(i + 1, j)
            dfs(i, j + 1)
        
        visited = []
        memory = {}
        dfs(0, 0)
        return len(visited)

方法二：DFS + 数位和改进

  class Solution:
      def movingCount(self, m: int, n: int, k: int) -> int:
          def dfs(i, j, si, sj):
              if i >= m or j >= n or k < si + sj or (i, j) in visited: return 0
              visited.add((i,j))
              return 1 + dfs(i + 1, j, si + 1 if (i + 1) % 10 else si - 8, sj) \
                       + dfs(i, j + 1, si, sj + 1 if (j + 1) % 10 else sj - 8)
  
          visited = set()
          return dfs(0, 0, 0, 0)

方法三： BFS + 数位和改进

class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        queue, visited,  = [(0, 0, 0, 0)], set()
        while queue:
            i, j, si, sj = queue.pop(0)
            if i >= m or j >= n or k < si + sj or (i, j) in visited: continue
            visited.add((i,j))
            queue.append((i + 1, j, si + 1 if (i + 1) % 10 else si - 8, sj))
            queue.append((i, j + 1, si, sj + 1 if (j + 1) % 10 else sj - 8))
        return len(visited)