面试题19. 正则表达式匹配【困难】

题目描述

做题链接：面试题19. 正则表达式匹配【困难】

设计一个函数用来实现正则表达式

解题思路

本题的【Hard】模式，正是因为考虑的情形比较多，很容易一些小细节漏做。尽管整理的时候已经是二次刷题了，但是还是花了 1H 调试+重写才成功

方法一：正查递归

考虑到的情况

ab <--> ab
ab <--> .*
ab* 的时候，b 零次的信息很容易漏掉
终止条件： if not p: return not a
判断相等逻辑： p[0] in {s[i], '.'}

方法二：倒查递归

倒查递归，思路参考 https://leetcode-cn.com/problems/zheng-ze-biao-da-shi-pi-pei-lcof/solution/zhu-xing-xiang-xi-jiang-jie-you-qian-ru-shen-by-je/

正则串是正常字符串匹配/. s[:n-2] p[:m-2]
正则串带 * a. 先直接去除 c* s,p[:m-2] b. 如果匹配*前的字符串， s[:n-1] p
正常字符串不匹配直接返回False

方法三：动态规划

作者：z1m

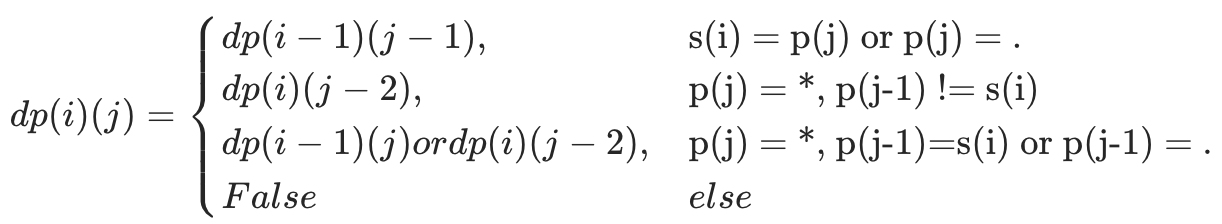
链接：https://leetcode-cn.com/problems/zheng-ze-biao-da-shi-pi-pei-lcof/solution/hui-su-dong-tai-gui-hua-by-ml-zimingmeng/

$$ dp(i)(j) = \ \left{ \begin{array}{l} \begin{matrix} dp(i - 1)(j - 1) ,& s(i)= p(j) \ or \ p(j) = .\ \end{matrix} \

\begin{matrix} dp(i - 1)(j - 2) ,& p(j) = * \ , \ p(j-1) != s(i)\ \end{matrix} \

\begin{matrix} dp(i - 1)(j) \ or \ dp(i)(j -2),& p(j) = * \ , \ p(j - 1) = s(i) \ or \ p(j - 1) = . \ \end{matrix} \

\begin{matrix} False ,& else \end{matrix} \

\end{array} \right. $$

代码

方法一：递归（Ugly）

class Solution:
      def isMatch(self, s: str, p: str) -> bool:
          if not p: return not s
          # ab <--> a* 带星号的一定要先处理，不然在 s='' p='*b'的时候会出错
          if len(p) > 1 and p[1] == '*':
               if self.isMatch(s, p[2:]): return True # 零次情况考虑到
               i = 0
               while i < len(s) and p[0] in {s[i], '.'}: # aaab a*b
                  if self.isMatch(s[i+1:], p[2:]): return True 
                  i += 1
          if p and s and p[0] in {s[0], '.'}: # ab <--> ab
               return self.isMatch(s[1:], p[1:])
          return False

方法一：递归（Graceful）

于此，我们又发现可以改进的地方

while i < len(s) and p[0] in {s[i], '.'}: # aaab a*b
     if self.isMatch(s[i+1:], p[2:]): return True 

可以列一张表，看到这里的 while 循环是不必要的，因为递归程序会帮我们一次次最终走到 * 三次 的情况，不需要我们自己显式的去写出，而且就算写出了，程序也走不到。

	s	p	value
原始	aaab	a*b	True
* 零次	aaab	b	False
* 一次	aab	b	False--> * 二次
* 二次	ab	b	False-->* 三次
* 三次	b	b	True

class Solution:
      def isMatch(self, s: str, p: str) -> bool:
          if not p: return not s
          # ab <--> a* 带星号的一定要先处理，不然在 s='' p='*b'的时候会出错
          if len(p) > 1 and p[1] == '*':
               if self.isMatch(s, p[2:]): return True # 零次情况考虑到
               if p and s and p[0] in {s[0], '.'} and self.isMatch(s[1:], p): return True 
          if p and s and p[0] in {s[0], '.'}: # ab <--> ab
               return self.isMatch(s[1:], p[1:])
          else:
               return False

Go示例

func isMatch(s string, p string) bool {
    if p == "" {
        return s == ""
    } 

    if len(p) > 1 && p[1] == '*' {
        if isMatch(s, p[2:]) { // 情况1: b a*b -> b b
            return true 
        }
        if len(s) > 0 && (s[0] == p[0] || p[0] == '.') {
            return isMatch(s[1:], p) // 情况2: aa a* -> a a* -> '' a* -> '' ''
        }
    }

    if len(s) > 0 && (s[0] == p[0] || p[0] == '.') {
        return isMatch(s[1:], p[1:])
    }
    return false
}

方法一：大神精简代码

# 作者：z1m
# 链接：https://leetcode-cn.com/problems/zheng-ze-biao-da-shi-pi-pei-lcof/solution/hui-su-dong-tai-gui-hua-by-ml-zimingmeng/

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        if not p: return not s
        # 第一个字母是否匹配
        first_match = bool(s and p[0] in {s[0],'.'})
        # 如果 p 第二个字母是 *
        if len(p) >= 2 and p[1] == "*":
            return self.isMatch(s, p[2:]) or \
            first_match and self.isMatch(s[1:], p)
        else:
            return first_match and self.isMatch(s[1:], p[1:])

方法二：倒查递归

def isMatch(self, s: str, p: str) -> bool:
        if not p : return not s
        if s and p[-1] in {s[-1], '.'}: 
            return self.isMatch(s[:-1], p[:-1])
        
        if p[-1] == '*':
            return self.isMatch(s, p[:-2]) or \
                   bool(s and p[-2] in {s[-1], '.'} and self.isMatch(s[:-1], p))
        return False

Go示例

func isMatch(s string, p string) bool {
    if p == "" {
        return s == ""
    }

    if len(s) > 0 && (p[len(p) - 1] == s[len(s) - 1] || p[len(p) - 1] == '.') {
        return isMatch(s[: len(s) - 1], p[: len(p) - 1])
    }

    if p[len(p) - 1] == '*' { // a a*
        if isMatch(s, p[: len(p) - 2]) {
            return true
        }
        
        // b .*
        if len(s) > 0 && (p[len(p) - 2] == '.' || p[len(p) - 2] == s[len(s) - 1]) {
            return isMatch(s[: len(s) - 1], p) 
        }
    }
    return false 
}

方法三：动态规划

func isMatch(s string, p string) bool {
    n, m := len(s), len(p)
  	// 边界条件，考虑 s 或 p 分别为空的情况
    if m == 0 {
        return n == 0
    }

    dp := make([][]bool, n + 1)
    for i := 0; i <= n; i++ {
        dp[i] = make([]bool, m + 1)
    }

    // base case : s == "", p == "" 
    dp[0][0] = true 
    
    for i := 0; i <= n; i++ { // i 是从0开始，因为可能存在s是""
        for j :=1; j <= m; j++ { // j 是从1开始，因为 j=0 的情况已经考虑过了
            l, r := i - 1, j - 1 // 因为 0 代表是空字符，所以 i 对应的字符是 i-1 的位置
            if p[r] == '*' {
                dp[i][j] = dp[i][j] || dp[i][j - 2] // situation1: aa a* -> aa ""
                //这里没有写 r-1>=0 ，因为 r 是 *，题意保证了 r-1>=0
                if l>=0 && (p[r - 1] == s[l] || p[r - 1] == '.') { // situation2: aa a* -> a a* -> '' a*
                    dp[i][j] = dp[i][j] || dp[i - 1][j]
                }
              // 这里没有写 r>=0，因为j的范围是从1开始，保证了 r>=0
            } else if l>=0 && (s[l] == p[r] || p[r] == '.') { // situation3: ba bc -> a c
                dp[i][j] = dp[i][j] || dp[i - 1][j - 1]
            }
        }
    }
    return dp[n][m]
}

题目描述​

解题思路​

方法一： 正查递归​

方法二： 倒查递归​

方法三：动态规划​

代码​

题目描述

解题思路

方法一：正查递归

方法二：倒查递归

方法三：动态规划

代码