面试题16. 数值的整数次方

题目描述

做题链接： 面试题16. 数值的整数次方

实现数值的整数次方。不得使用库函数，同时不需要考虑大数问题。

解题思路

方法一： 快速幂

二分推导：

• 当 n 为偶数： $x^n=x^{n/2}\times x^{n/2}$
• 当 n 为奇数： $x^n=x^{n/2}\times x^{n/2}\times x$

时间复杂度为 $O(log_2n)$ 空间复杂度 $O(1)$

方法二：数学递推法 + 位运算

举例 $n = 9$ ，用二进制可表示为 $n = 9 = 1001_b$ $$ x^9 = 1\times x^{2^0} \times x^{2^3} $$ 这里，发现 $x^{2^0} = y$， 此时公式就变成 $$ x^9 = 1\times y \times y^3 $$ 可以发现，只要对应二进制位为 0 的话，就不乘上去。

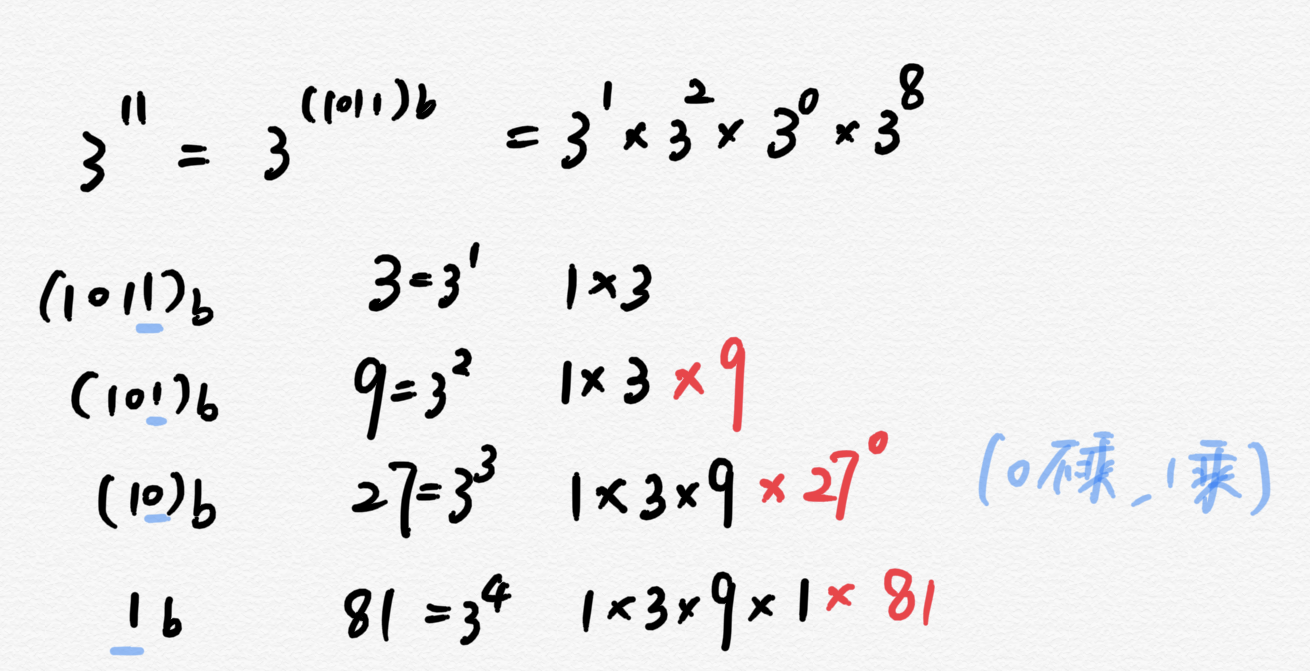
代码

方法一：快速幂

class Solution:
    def myPow(self, x: float, n: int) -> float:
        if n == 0: return 1
        if n == 1: return x
        pos_n = abs(n)
        temp = self.myPow(x, pos_n >> 1)
        res = temp * temp * (x if pos_n & 1 else 1)
        return res if n > 0 else 1/res 

方法二：数据递推法 + 位运算

class Solution:
      def myPow(self, x: float, n: int) -> float:
          pos_n = abs(n)
          res = 1
          while pos_n:
              res = res * (x if (pos_n & 1) else 1)
              pos_n = pos_n >> 1
              x = x * x
          return res if n > 0 else 1/res